기본 용어
릴레이션
- 관계형 데이터베이스에서 정보를 구분하여 저장하는 기본 단위
- DB 테이블이라 할 수 있음
릴레이션의 특징
- 한 릴레이션에는 똑같은 투플(Tuple)이 포함될 수 없으므로 릴레이션에 포함된 투플들은 모두 상이하다.
- 한 릴레이션에 포함된 투플 사이에는 순서가 없다.
- 투플들의 삽입, 삭제 등의 작업으로 인해 릴레이션은 시간에 따라 변한다.
- 릴레이션 스키마를 구성하는 속성들 간의 순서는 중요하지 않다.
- 속성의 유일한 식별을 위해 속성의 명칭은 유일해야 하지만, 속성을 구성하는 값은 동일한 값이 있을 수 있다.
- 릴레이션을 구성하는 투플은 유일하게 식별하기 위해 속성들의 부분집합 키(Key)로 설정한다.
- 속성의 값은 논리적으로 더 이상 쪼갤 수 없는 원자 값만을 저장한다.
속성(attribute, 어트리뷰트)
- 개체(entity)의 항목들
- 사물이 될 수 도 있고, 추상적인 개념이 될 수도 있음
- 동일 릴레이션 내에서는 같은 이름의 속성이 존재할 수 없음
- 하나의 열은 하나의 속성 정보를 표시
- 예를 들어, 아래와 같은 학생 릴레이션이 있다고 가정했을 때 속성은 학번, 이름, 학년, 전공, 점수 가 된다.

차수(degree)
- 한 릴레이션 안에 있는 어트리뷰트의 수
- 유효한 릴레이션의 최소 차수는 1
- 따라서, 모든 릴레이션은 적어도 하나 이상의 어트리뷰트를 갖고 있음을 알 수 있음.
투플(tuple, 레코드)
- 릴레이션의 각 행을 레코드 또는 투플이라고 함.
카디날 리티(Cardinality)
- 릴레이션 튜플의 개수
- 데이터가 삽입되지 않은 테이블의 경우 카디날 리티는 차수와 다르게 0의 값을 가질 수 있음
- 시간에 따라 값이 계속해서 변함
도메인(domain)
- 릴레이션에 포함된 속성들이 각각 가질 수 있는 값들의 집합
- 예를 들어
- “안경 착용 유무”라는 속성이 있을 때, 이 속성의 값은 “유” 또는 “무”
- 이 집합 ( ”유”, “무”)의 이름을 A라고 지정했을 때
- “안경 착용 유무”라는 속성은 도메인 A에 있는 값만 가질 수 있게 되는 것
- 도메인 이름은 속성 이름과 같을 수도 있고 다를 수도 있음
- 하나의 도메인을 여러 속성에서 공유 가능
스키마
- 데이터베이스의 구조와 제약 조건에 관한 전반적인 명세를 기술한 메타데이터의 집합
- 데이터베이스를 구성하는 개체(Entity), 속성(Attribute), 관계(Relationship) 및 데이터 조작 시 데이터 값들이 갖는 제약 조건 등에 관해 전반적으로 정의함.
- 사용자의 관점에 따라 외부 스키마, 개념 스키마, 내부 스키마로 나뉨.

논리 모델 vs 물리 모델
| 논리모델 | 물리모델 |
| 엔티티(Entity) | 테이블(Table) |
| 속성, 어트리뷰트(Attribute) | 컬럼(Column) |
| 관계, 릴레이션(Relation) | 관계, 릴레이션(Relation) |
| 키 그룹(Key group) | 인덱스(Index |
관계 데이터 모델에서 지원되는 두 가지 정형적인 언어
- 관계 해석(relational calculus) - What
- 원하는 데이터만 명시하고 질의를 어떻게 수행할 것인가는 명시하지 않는 선언적인 언어
- 관계 대수(relational algebra) - How
- 어떻게 질의를 수행할 것인가를 명시하는 절차적 언어
- 관계 대수는 상용 관계 DBMS들에서 널리 사용되는 SQL의 이론적인 기초
- 관계 대수는 SQL을 구현하고 최적화하기 위해 DBMS의 내부 언어로서도 사용됨
SQL
- 상용 관계 DBMS들의 사실상의 표준 질의어인 SQL을 이해하고 사용할 수 있는 능력은 매우 중요함
- 사용자는 SQL을 사용하여 관계 데이터베이스에 릴레이션을 정의하고, 관계 데이터베이스에서 정보를 검색하고, 관계 데이터베이스를 갱신하며, 여러 가지 무결성 제약조건들을 명시할 수 있음
관계 대수
- 기존의 릴레이션들로부터 새로운 릴레이션을 생성함
- 릴레이션이나 관계 대수식 (이것의 결과도 릴레이션임)에 연산자들을 적용하여 보다 복잡한 관계 대수식을 점차적으로 만들 수 있음
- 기본적인 연산자들의 집합으로 이루어짐
- 산술 연산자와 유사하게 단일 릴레이션이나 두 개의 릴레이션을 입력으로 받아 하나의 결과 릴레이션을 생성함
- 결과 릴레이션은 또 다른 관계 연산자의 입력으로 사용될 수 있음

관계 연산자

- 유도된 연산자: 필수적인 연산자를 이용하여 유도된 연산자, 필수 연산자만을 이용하여 표현 가능 하지만 자주 사용되기 때문에 제안됨.

Selection 연산자
- 한 릴레이션에서 Selection 조건을 만족하는 투플들의 부분 집합을 생성함
- 단항 연산자
- 결과 릴레이션의 차수는 입력 릴레이션의 차수와 같음
- 결과 릴레이션의 카디날 리티는 항상 원래 릴레이션의 카디날 리티보다 작거나 같음
- Selection 조건을 프레디 키드(predicate)라고도 함
- Selection 조건은 일반적으로 릴레이션의 임의의 어트리뷰트와 상수, =, <>, ≤, <, ≥, > 등의 비교 연산자, AND, OR, NOT 등의 부울 연산자(논리 연산자)를 포함할 수 있음
Projection 연산자
- 한 릴레이션의 어트리뷰트들의 부분 집합을 구함
- 결과로 생성되는 릴레이션은 <어트리뷰트 리스트>에 명시된 어트리뷰트들만 가짐
- Selection의 결과 릴레이션에는 중복 투플이 존재할 수 없지만, Projection 연산의 결과 릴레이션에는 중복된 투플이 존재할 수 있음
*Selection의 경우 처음부터 원하는 조건으로 검색한 결과를 나타내기 때문에 그 자체로 유니크해서 중복이 존재하지 않음
집합 연산자
- 릴레이션이 투플들의 집합이기 때문에 기존의 집합 연산이 릴레이션에 적용됨
- 세 가지 집합 연산자: 합집합, 교집합, 차집합 연산자
- 집합 연산자의 입력으로 사용되는 두 개의 릴레이션은 합집합 호환(Union compatible)이어야 함.
- 이항 연산자
- 결과 릴레이션의 차수는 R 또는 S의 차수와 같으며, 결과 릴레이션의 어트리뷰트 이름들은 R의 어트리뷰트들의 이름과 같거나 S의 어트리뷰트들의 이름과 같음
합집합 호환
- 두 릴레이션 R1(A1, A2,.. An)과 R2(B1, B2,... Bm)이 합집합 호환일 필요충분조건은 n=m이고, 모든 1≤ i ≤ n에 대해 domain(Ai) = domain(Bi)이어야 함.
- 어트리뷰트의 수(차수): n, m
합집합 연산자
- 두 릴레이션 R과 S의 합집합 R U S는 R 또는 S에 있거나 R과 S 모두에 속한 투플들로 이루어진 릴레이션
- 결과 릴레이션에서 중복된 투플들은 제외됨
교집합 연산자
- 두 릴레이션 R과 S의 교집합 R ∩ S는 R과 S 모두에 속한 투플들로 이루어진 릴레이션
차집합 연산자
- 두 릴레이션 R과 S의 차집합 R - S는 R에는 속하지만 S에는 속하지 않은 투플들로 이루어진 릴레이션
카디션 곱 연산자
- 카디날 리티가 i인 릴레이션 R(A1, A2, ... An)과 카디날리티가 j인 릴레이션 S(B1, B2,..., Bm)의 카디션 곱 R X S는 차수가 n+m이고, 카디날리티가 i * j 이고, 어트리뷰트가 ( A1, A2, ..., An, B1, B2, ... Bm )이며, R과 S의 투플들이 모든 가능한 조합으로 이루어진 릴레이션
- 카티션 곱의 결과 릴레이션의 크기가 매우 클 수 있으며, 사용자가 실제로 원하는 것은 카티션 곱의 결과 릴레이션의 일부인 경우가 대부분이므로 카티션 곱 자체는 유용한 연산자가 아님

관계 대수의 완전성
- Selection, Projection, Union, difference, Cartesian product는 관계 대수의 필수적인 연산자
- 다른 관계 연산자들은 필수적인 관계 연산자를 두 개 이상 조합하여 표현할 수 있음
- 임의의 질의어가 적어도 필수적인 관계 대수 연산자들만큼의 표현력을 갖고 있으면 관계적으로 완전(Relationally Complete) 하다고 함. → 쉽게 말해서, 필수 연산자를 전부 표현할 수 있으면!
조인 연산자
- 두 개의 릴레이션으로부터 연관된 투플들을 결합하는 연산자
- 관계 데이터베이스에서 두 개 이상의 릴레이션들의 관계를 다루는데 매우 중요한 연산자
- 종류
- 세타 조인(theta join) : 6가지의 비교 연산자중 하나를 사용하여 조인
- 동등 조인(equi join) : 비교연산자 중 ‘=’를 이용한 조인, 두 릴레이션의 같은 어트리뷰트를 묶음으로서 결과 릴레이션에 조인에 사용됐던 어트리뷰트가 2개 생성됨
- 자연 조인(natural join) : 동등 조인에서 중복된 어트리뷰트 값 중 하나를 제외시킨 조인, 가장 많이 사용됨
- 외부 조인(outer join)
- 세미 조인(serni join) 등
세타 조인과 동등 조인
- 두 릴레이션 R( A1, A2,..., An)과 S(B1, B2,..., Bm)의 세타 조인의 결과는 차수가 n+m이고, 어트리뷰트가 (A1, A2, ..., An, B1, B2, ..., Bm)이며, 조인 조건을 만족하는 투플들로 이루어진 릴레이션
- 세타는 ‘=’, ‘<>’, ‘≤’, ‘<’, ‘≥’, ‘>’ 중에 하나
- 동등 조인은 세타 조인 중에서 비교 연산자가 ‘=’인 조인
*비교 연산자 ’<>’ = ‘≠’
동등 조인 예
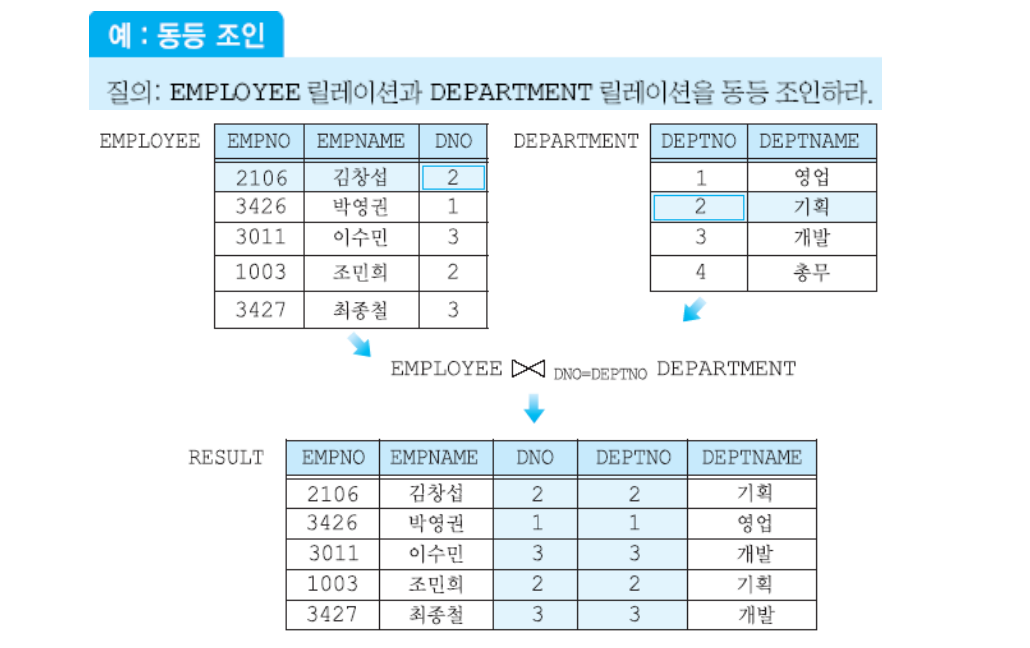
- 주로 공통된 어트리뷰트를 이용하여 조인이 이루어짐.
- 공통된 어트리뷰트가 없는데 조인을 하는 것은 아무 의미가 없는 것임.
자연 조인

- 동등 조인의 결과 릴레이션에서 조인 어트리뷰트를 제외한 조인
- 여러 가지 조인 연산자들 중에서 가장 자주 사용됨
- 실제로 관계 데이터베이스에서 대부분의 질의는 Selection, Projection, 자연 조인으로 표현 가능
디비전 연산자
- 차수가 n+m인 릴레이션 R( A1, A2,... An, B1, B2,... , Bm )과 차수가 m인 릴레이션 S(B1, B2,..., Bm)의 디비전 R / S는 차수가 n이고, S에 속하는 모든 투플 u에 대하여 투플 tu( 투플 t와 투플 u를 결합한 것)가 R에 존재하는 투플 t들의 집합

- Result 1: 초기 릴레이션 AB에서 릴레이션 C의 투플인 b1을 갖고 있는 투플의 집합
- Result 2: 초기 릴레이션 AB에서 릴레이션 C의 투플인 b2, b4를 모두 갖고 있는 투플의 집합
- Reuslt 3: 초기 릴레이션 AB에서 릴레이션 C의 투플인 b1, b2, b3를 모두 갖고 있는 투플의 집합
관계 대수의 질의

관계 대수의 한계
- 관계 대수는 산술 연산을 할 수 없음
- 집단 함수(aggregate function)를 지원하지 않음 →ex) 통계 연산 등
- 정렬을 나타낼 수 없음
- 데이터베이스를 수정할 수 없음
- 프로젝션 연산의 결과에 중복된 투플을 나타내는 것이 필요할 때가 있는데 이를 명시하지 못함
추가된 관계 대수 연산자
- 집단 함수 ( 평균 등 )
- 그룹화
- 외부 조인
외부 조인
- 상대 릴레이션에서 대응되는 투플을 갖지 못하는 투플이나 조인 어트리뷰트에 널 값이 들어 있는 투플들을 다루기 위해서 조인 연산을 확장한 조인
- 두 릴레이션에서 대응되는 투플들을 결합하면서, 대응되는 투플을 갖고 있지 않는 투플과 조인 어트리뷰트에 널 값을 갖는 투플도 결과에 포함 시킴
- 왼쪽 외부 조인( left outer join), 오른쪽 외부 조인( right outer join ), 완전 외부 조인( full outer join)
왼쪽 외부 조인
- 릴레이션 R과 S의 왼쪽 외부 조인 연산은 R의 모든 투플들을 결과에 포함시키고, 만일 릴레이션 S에 관련된 투플이 없으면 결과 릴레이션에서 릴레이션 S의 어트리뷰트들은 널값으로 채움

오른쪽 외부 조인
- 왼쪽 외부 조인과 반대

완전 외부 조인
- 릴레이션 R과 S의 완전 외부 조인 연산은 R과 S의 모든 투플들을 결과에 포함시키고, 만일 상대 릴레이션에 관련된 투플이 없으면 결과 릴레이션에서 상대 릴레이션의 어트리뷰트들은 널값으로 채움

출처
'Computer Science > DataBase' 카테고리의 다른 글
| 뷰와 시스템 카탈로그(1) (0) | 2022.04.20 |
|---|---|
| 릴레이션 정규화 (0) | 2022.04.20 |
| 물리적 데이터베이스 설계 (0) | 2022.04.15 |
| 데이터베이스 설계와 ER모델(2) (0) | 2022.04.13 |
| 데이터베이스 설계와 ER 모델(1) (0) | 2022.04.13 |



